


Next: More Examples
Up: predCalcIntro
Previous: predCalcIntro
The language of predicate calculus consists of:
- SYMBOLS
- Variable symbols: x, y, z ...
- Function symbols: f, g, h ...
- Predicate symbols: P, Q, R, ...
- Logic symbols
- Connectives:
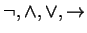
- Quantifiers:

- TERMS
- Constant: a, b, c ...
- Variables
- f(T) where f is a function and T is a term
- Examples: f(a,x) g(x, f(a,x))
- ATOMIC FORMULAS (also called Propositions)
- True and False
- P(T) where P is a predicate (T is a term)
- LITERALS
- Atomic formulas
- Negated atomic formulas
- WELL-FORMED FORMULAS (WFFS - also called sentences)
- A predicate applied to the correct number of terms
- If P and Q are formulas then these are wffs:
- If x is a variable, and P is a formula, then the following are wffs:
- SENTENCES
- A wff with all variables in the scope of corresponding quantifiers
- Examples:
- Sentence
![$ \forall x[Feathers(x) \rightarrow Bird(x)]$](img9.gif)
- Not a sentence:
![$ \forall x[Feathers(x) \vee Feathers(y)] $](img10.gif)
because y is a free variable
- VALID: something is always true (Tautology)
- SATISFIABLE: something which has at least one set of values to make it true
- UNSATISFIABLE: something which is never true (Contradiction)



Next: More Examples
Up: predCalcIntro
Previous: predCalcIntro
Randy Latimer
2001-01-02
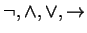

![$ \forall x[Feathers(x) \rightarrow Bird(x)]$](img9.gif)
![$ \forall x[Feathers(x) \vee Feathers(y)] $](img10.gif)