Predicate Calculus Example (p. 166-168 Tanimoto)

Translate the following into predicate calculus:

Any normal bird can fly. An ostrich is an abnormal bird. A whirlybird is not a normal bird, either. A whirlybird is not even a bird. Anything that's not an abnormal bird must either be a normal bird or a whirlybird. Tweety is a bird, but not a normal bird. Tweety has her wings clipped. Tweety has two parents. They are normal birds.

Steps to take:

1. Refine the English into separate, expanded statements
2. Identifying the domain
3. Identifying the constants
4. Structuring the domain - finding important subsets of the domain
5. Identifying and expressing functional relationships
6. Writing predicates to represent relationships
7. Identifying and expressing logical relationships
8. Identifying and expressing quantification over parts of the domain

Here's the process of translating the sentences into predicate calculus:

Step 1: rewrite the English to emphasize quantified propositions and omit rhetorical features irrelevant to the logical meaning of the text.

Every normal bird can fly. An ostrich is a bird, and not a normal bird. A whirlybird is not a normal bird. A whirlybird is not a bird. Every object that is not a bird that is not normal is either a normal bird or a whirlybird. Tweety is a bird. Tweety is not a normal bird. Tweety has her wings clipped. There exist precisely two individuals that are parents of tweety, and they are both normal birds.

Step 2: Identify the domain: class of birds and the class of whirlybirds (helicopters)

Step 3: Identify the constants: Tweety

Step 4: Structure the domain: birds, normal birds, abnormal birds (birds that are not normal), female birds, the parents of Tweety, and the whirlybirds.

Step 5: Using predicates to express functional relationships.

Parent(x, Tweety)

Bird(x)

Normal(x)

Female(x)

Whirlybird(x)

Clipped-wings(x).

Step 6: Identify the quantifications in the statements and over what parts of the domain the quantifications are valid.

For example: "Every normal bird..." $\forall x[(Bird(x) \bigvee Normal(x)) \Rightarrow. . . ]$

Here is the translation:

1. $\forall x[(Bird(x) \bigwedge Normal(x)) \Rightarrow CanFly(x)]$
2. $\forall x[(Ostrich(x) \Rightarrow (Bird(x) \bigwedge \neg Normal(x))]$
3. $\forall x[(Whirlybird(x) \Rightarrow \neg (Bird(x) \bigwedge Normal(x))]$
4. $\forall x[(Whirlybird(x) \Rightarrow \neg Bird(x)]$
5. $\forall x[(\neg Bird(x) \bigwedge \neg Normal(x)) \Rightarrow ((Normal(x) \bigwedge Bird(x)) \bigvee Whirlybird(x))]$
6. $Bird(Tweety)$
7. $\neg Normal(Tweety) \bigwedge Bird(Tweety))$
8. $ClippedWings(Tweety)$
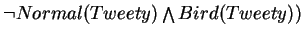
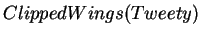
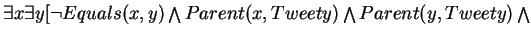
9. $\exists x \exists y[\neg Equals(x,y) \bigwedge Parent(x,Tweety) \bigwedge Parent(y,Tweety) \bigwedge$ $[\forall z(Parent(z,Tweety) \Rightarrow (Equals(z,x) \bigvee Equals(z,y)))]]$
10. $\forall x[(Parent(x, Tweety) \Rightarrow (Normal(x) \bigwedge Bird(x))]$