Truth-Functional Translation Tips

1. Bivalence.
   While there are 3-valued and many-valued logics, our logic is 2-valued (or bivalent). Therefore, "She was not unhappy" must be translated as if it were synonymous with "She was happy".

2. Exclusive disjunction
   Remember that $\vee$ is disjunction: it means that either p is true or q is true or both.
   The exclusive disjuntion (XOR:$\oplus$) of p and q asserts that either p is true or q is true but not both.
   $(p \vee q) \wedge \neg(p \wedge q)$

3. Conjuction
   We express conjuction with many words other than "and", including "but", "moreover", "however", "although", and "even though".
   Bert and Ernie are brothers cannot be translated into "Bert is a brother and Ernie is a brother".

4. "Unless"
   Example: You won't do well unless you study
   Or
   If you do not study then you will not do well
   $\neg S \rightarrow \neg D$
   Which is logically equivalent to
   $S \vee \neg D$
   "p unless q" should be translated either as
   $p \vee q$ (inclusive disjunction) or as $p \oplus q$ (exclusive disjunction)

5. "And/or"
   Translate as inclusive disjunction:
   "Bring a scarf and/or hat" means 'bring a scarf or hat or both"
   Translated: $S \vee H$

6. "Neither, nor"
   "Neither p nor q" means that both p and q are false.
   Translated: $\neg p \wedge \neg q$ or $\neg(p \vee q)$ (equivalent formulas by DeMorgan's Th.)

7. "Not both/ both not"
   "p and q not both true": this means a denial of the conjunction,
   $\neg (p \land q)$. One of them may be true, but not both.
   This is also equivalent to: $\neg p \lor \neg q\\$

   "p and q are both not true" means that neither may be true:
   $\neg p \wedge \neg q$ which is also equivalent to $\neg (p \lor q)$
   

   More examples:
   "Kim and Jim do not both like goats".
   This is a negation of the conjunction:"Both Kim and Jim like goats":
   $\neg(K \land J)$
   

   "Both Kim and Jim do not like goats":
   $\neg K \land \neg J''$
   Note: This "both not" statement is the same as "neither nor"
   "Both Kim and Jim do not like goats" is the same as
   "Neither Kim nor Jim likes goats":
   $\neg K \land \neg J$
   

8. Material Implication: $p \rightarrow q$
   $p \rightarrow q$ translates into a wide variety of English expressions:
   • "if p, q", "p implies q", "p entails q"
   • "p therefore q", "p hence q", "since p, q", "because p, q",
   • "q if p", "q provided p", "q since p", "q because p"
   • "q follows from p", " p is the sufficient condition of q"
   • "q is the necessary conditon of p"
   • Least intuitive: "p only if q"

9. Necessary and Sufficient Conditions
   Sufficient conditon: p is a sufficient condition of q when p's truth guarantees q's truth.
   Necessary condition: q is a necessary conditon of p when q's falsehood guarantees p's falsehood.
   In the ordinary implication: $p \rightarrow q$, the antecedent p is a sufficient condition of the consequent q, and the consequent q is a necessary conditon of the antecedent p.
   
   • Modus ponens: Given 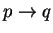$p \rightarrow q$, the truth or presence of p suffices to give us q.
     Hence the antecedent is the sufficient condition of the consequent.
     
   • Modus tollens: Give 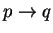$p \rightarrow q$, the falsehood of q (the truth of 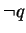$\neg q$) guarantees the falshood of p (the truth of $\neg p$)
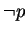     Hence the consequent is the necessary conditon of the antecedent
     
   • Example: "If Socks is a cat, then Socks is a mammal"
     Being a cat is a sufficient conditon of being a mammal.
     Being a mammal is a necessary condition of being a cat.
     
   • If p is both necessary and sufficient for q, then "$p \equiv q$"
     

10. "Only if"
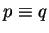    "p only if q" is translated as: $p \rightarrow q$
    

    Example: "You will win only if you have a ticket"
    $T \rightarrow W$ is not correct: "If you have a ticket then you will win".
    $W \rightarrow T$ is correct: "If you win then you have a ticket."
    

    Example: "A car will run only if there is gas in the tank"
    Equivalent to "If a car will run, then there is gas in the tank"
    

11. "if and only if"
    Analysis: "p only if q" is $p \rightarrow q$ and "p if q" is $q \rightarrow p$
    Therefore "p if and only if q" is $p\leftrightarrow q$
    

    Translated also as "iff"
    

12. "Just when"
    "p just when q" means p is true when and only when q is true, or
    p is true if and only if q is true
    $p\leftrightarrow q$
    

13. "Even if"
    "p even if q" means "p whether or not q" or "p regardless of q".
    Therefore this could be translated simply as "p".

14. Truth functionality (see handout)

15. Puctuation (see handout)

16. Specific form (see handout)
17. Play (see handout)
18. Canonical quantitative propositions (see the previous section)

19. Quantifier scope
    The scope of a quantifier is like the scope of a negation sign:
    the first whole proposition, or propositional function, to its right
    

    $(\forall x) A(x) \rightarrow B(x)$ means $[(\forall x)A(x)] \rightarrow B(x)$
    THIS DOES NOT MEAN: $(\forall x)(A(x) \rightarrow B(x))$
    

    Alternate notations: $\forall xA(x)\rightarrow B(x)$ and $\forall x Ax \rightarrow Bx$
    

20. "Some" (see handout)

    Inclusive use of "some":
    Existential quantifier, $\exists$, expresses the inclusive use of "some
    "Some of you will earn an A on the final exam" means at least one and
    possibly all of you will earn an A.
    

    Exclusive use of "some":
    Translated as "not all" (see tips 18,33)
    $(\exists x) (Mx \land \neg Ex)$ says that there is at least one M&M she does not eat.
    

21. "Only some" (see handout)
    Means "more than one and less than all" or "neither none nor all"
    

22. Which quantifier? (see handout)
    
23. Avoid the negative (see handout)
    
24. Universe of discourse (see handout)
25. Limiting the universe of discourse (see handout)
    Example: "All humans are mortal"...
    Too strong of an interpretation: $\forall x M(x)$ means everything is mortal.
    Better interpretation: $\forall x (Hx \rightarrow Mx)$

26. Translating "and" as "or"
    Be prepared to translated "and" as "or".
    For example, "Men and women are welcome to apply".
    THIS IS NOT: $(\forall x)[(Mx \land Wx) \rightarrow Ax]$
    Correct interpretation is $(\forall x) [(Mx \lor Wx) \rightarrow Ax]$
    Also see handout

27. Universal quantifiers, $\forall$, typically take conditionals
    Example: "All humans are mortal": $\forall x (Hx \rightarrow Mx)$
    NOT: $(\forall x)(Hx \land Mx)$ This means everything in the universe is mortal,
    even my chalk.
    Also see handout

28. Existential quantifiers, $\exists$, typically take conjunctions
    Example:"Some humans are inhumane" means $(\exists x)(Hx \lor Ix)$

29. Avoid existentially quantified conditionals
    "If something falls into a black hole, then it will be lost forever"
    Don't use: $(\exists x)(Bx \rightarrow Lx)$
    Better to use: $(\exists x)(\neg(Bx \lor Lx))$
    Also see handout
    

30. Names: Names should be treated as constants.
    "Elvis is alive" is simply "Ae"
    Don't make Elvis into a predicate: $(\exists x)(Ex \land Ax)$
    or into a variable: "(e)Ae"

31. Bind all your variables
    Example: "Somebody slept in my bed!" is $(\exists x) Sx$

32. "No A's are B's"
    Translate as : $(\forall x)(Ax \rightarrow \neg Bx)$
    which is equivalent to: $(\forall x)(Bx \rightarrow \neg Ax)$
    Also, see handout

33. "Not all/all not"
    "All that glitters is not gold" should be stated "Not all that glitters is gold"
    "All not" statements:
    Example: "All bats are not feathered": $(\forall x)\neg(Bx \rightarrow Fx)$ or translated as: $(\forall x)(Bx \rightarrow \neg F(x))$

    "Not all" statements:
    "Not all cars are lemons":
    Translate as $\neg (\forall x)(Cx \rightarrow Lx)$ or $(\exists x)(Cx \land \neg Lx)$.
    Also see handout.

34. "Only"
    "Only B's are A's" is equivalent to "All A's are B's"
    Translated as: $(\forall x)(Ax \rightarrow Bx)$
    Also see handout

35. "All and only" see handout

36. "None but"
    "None but ripe bananas are edible": $(\forall x)((Bx \land Ex) \rightarrow Rx)$

37. Indefinite articles, "a" and "an". See handout
    "A bat is a mammal" really means "All bats are mammals"
    Translated as: $(\forall x)(Bx \rightarrow Mx)$
    

38. Definite articles, "the". See handout
    Sometimes takes existential, sometimes universal quantifiers.
    "The horse is a noble animal" means "All horses are noble animals"
    Translated as $(\forall x)(Hx \rightarrow Nx)$
    

    "The horse in the winner's circle is on drugs" means "There exists a horse, the
    one in the winners circle, who is on drugs.
    Translated as $(\exists x)(Hx \land Wx \land Dx)$

39. "Any" sometimes existential, sometimes universal. See handout.
    "Any bat is a mammal means "All bats are mammals": $(\forall x)(Bx \rightarrow Mx)$
    

40. Puctuation. See Handout.