With the advent of ever more powerful computers, a new branch of science emerged -- Computational Science. Using computer simulations, scientists could explore areas they never could before, and the results were often amazing. The symbol of this movement was the supercomputer; like the mainframes of yore it had its own room, its own cooling system, and its own priesthood of attendants, but the supercomputer also posessed unparalleled processing power, making it the envy of many a lesser user.
However, for those of us without access to one of those munificent monoliths, there is still some hope. Many simpler problems are well within the capabilities of modern PCs. Take, for example, the problem of trying to hit a target with a projectile.
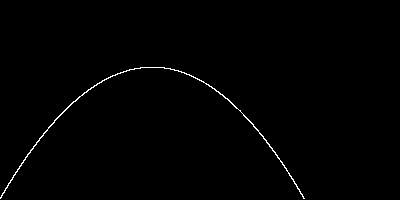
The first step to investigating the problem is to make a simple simulation of the situation1, and try a variety of launching angles and velocities, printing the trajectory to the screen. A sample trial looks like this:

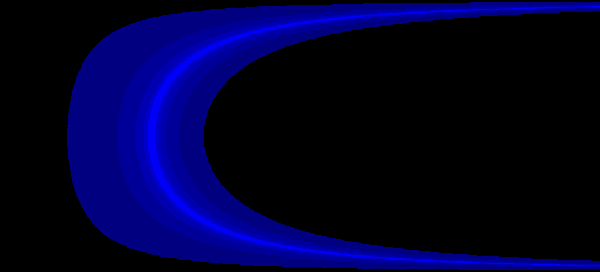
The next step is to try all the possible values. The picture below shows the results of shooting a projectile from 0 to 90 degrees (from bottom to top) and from 1 to 1000 meters per second (from left to right). It is trying to hit a target 2000 meters away, and the different colors show how far away it landed (they get dimmer exponentially).
Then, you want to change something with the simualtion, such as adding wind or a gravitational attractor. We decided to add walls. When a projectile hits a wall, it rebounds with its velocity halved. First we modified our original projectile firing program to test our ideas. Here is the same trial as the first with a wall added.
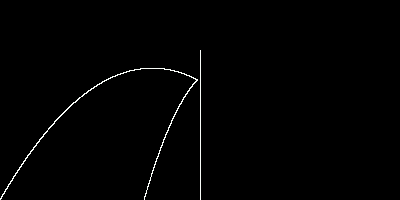
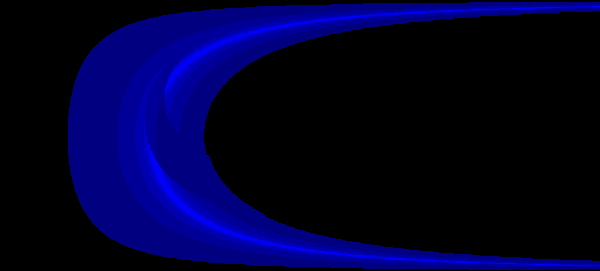
Then we changed the second program so that you could add walls. Here is a picture of the original simulation with a 400 meter tall wall floating 300 meters above 1500 meters away from the launching point.
Here is source code for the second through fourth programs mentioned above: program2, program3, program4
1For those of you interested in the physics of the simulation, the
equations we used were:
height = launch velocity * sin(launch angle) * time + .5 * g * time ^ 2
distance = launch velocity * cos(launch angle) * time