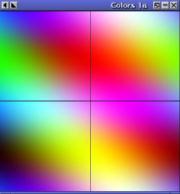
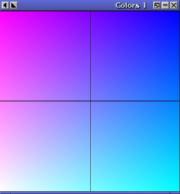
The following variables are predefined:
The following code essentially cycles through all pixel locations Compare the following two algorithms which produce exactly the same output. The second one is almost twice as fast because careful consideration is given to eliminate wasted computation.
Poor Algorithm
DrawGraph()
{ int i, j;
float x, y, xstep, ystep, r, g, b;
glBegin(GL_POINTS);
for (i=0; i<360; i++){
for (j=0; j<360; j++){
xstep = (xmax-xmin)/359.0;
ystep = (ymax-ymin)/359.0;
x = xmin + xstep * i;
y = ymin + ystep * j;
r = i / 360.0;
g = j / 360.0;
b = 1.0;
glColor3f(r, g, b);
glVertex3f(x, y, 0.0);
glFlush();
}
}
glEnd();
}
The complete program: colors1.c
|
CommentsIn this program, there is much wasted arithmetic. Multiplication and division are both "expensive" operations that require extra processor time, yet the variables xstep and ystep are never changed. It is important to find out how far apart adjacent pixels are, but these values are recalculated each time through the inner loop resulting in 360 times 360 divisions, or an amazing 129,600 division operations for each of those variables when only one was needed!The assignment of the blue component, b, never changes and the red component, r, only changes with the outer loop. It is unnecessary to do these operations repeatedly too. Function calls are also "expensive" operations. The function glFlush() forces the writing of pixels to the screen after each assignment, and thus the overhead of that function call another 129,600 times is unnecessarily extreme. The drawing buffer is never allowed to fill up with anything. A single call after all of the drawing is finished would have been sufficient. |
Better Algorithm
DrawGraph()
{ int i, j;
float x, y, xstep, ystep, r, g, b;
xstep = (xmax-xmin)/359.0;
ystep = (ymax-ymin)/359.0;
b = 1.0;
glBegin(GL_POINTS);
x = xmin;
for (i=0; i<360; i++){
r = i / 360.0;
y = ymin;
for (j=0; j<360; j++){
g = j / 360.0;
glColor3f(r, g, b);
glVertex3f(x, y, 0.0);
y += ystep;
}
x += xstep;
}
glEnd();
glFlush();
}
The complete program: colors1a.c
|
CommentsIn this program, the variables xstep and ystep have both been moved outside the main loop as well as the assignment of b.Instead of multiplying the the step variables by the loop indecies to determine the current pixel position, the variables x and y are assigned the initial values xmin or ymin respectfully, and then incremented by adding the step values onto a running total. It is necessary to reinitialize the y-value at each increment in the x-loop, but addition is much less time consuming than multiplication or division. The function glFlush() has been moved outside of the loop and after the code that plots GL_POINTS, so it is only called once. OpenGL will actually write most of the graph to the screen anyway as the buffer gets filled, but this function just forces the writing of any queued commands. |
The mathematical functions sine and cosine are excellent functions to use for this effect. Since these functions return values between +1 and -1, additional some minor modifications must be made to force them into the proper range between 0 and +1. One approach might be to apply the absolute value to these functions, but take a look at the code of the following program to see what was done.
Varying the RGB Values
glBegin(GL_POINTS);
x = xmin;
for (i=0; i<360; i++){
y = ymin;
for (j=0; j<360; j++){
r = 0.5 * (1 + sin( i / 90.0));
g = 0.5 * (1 + sin ( (i + j) / 60.0));
b = 0.5 * (1 + cos(j /30.0));
glColor3f(r, g, b);
glVertex3f(x, y, 0.0);
y += ystep;
}
x += xstep;
}
glEnd();
Complete Program: colors2b.c
|
CommentsThe sine function evaluates to zero at 0o and reaches its maximum value of 1 at 90o. Since the sine function in C++ expects radians instead of degrees, it is necessary to divide the integer i by some value to slow down the the rapid change that the red component, r, would see as the loop variable varies from 0 to 360. The sine also hits its minimum of -1 at 270o, so by adding 1 to the output of the sine function, and then multiplying by 0.5, the value is scaled back into the range of 0 to 1.In calculating the g value, a similar approach is made but the value used in the division is modified in order to change the period. The cosine function used in the calculation of the blue component of the color is similar to the sine approach, except that the cosine of 0o is 1 and it goes to zero when the angle reaches 90o. A different value of 30.0 is used for changing the period of than function.
These are not the only methods of changing the color ramp, but remember
to include the math libraries: |