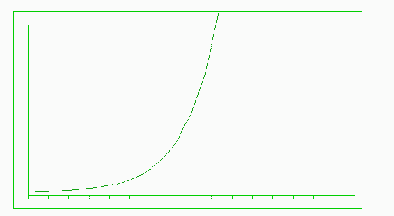
Figure #4: Exponential Curve
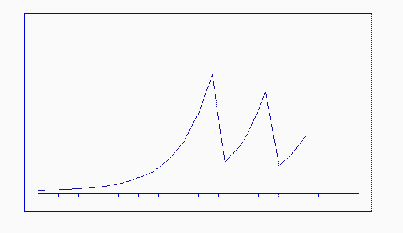
Figure #5: Oscillating Growth
Gypsy moths spread by several methods. Because females contain so many eggs, adult moths are too heavy to fly although they are able to crawl. Adults often lay egg masses on moveable objects such as automobiles or campers which then travel to other regions of the country. When these eggs hatch, a new infestation site becomes established.
At first, the young larva are quite small and can be blown by the wind on silk threads for distances up to ten miles. As caterpillars become larger, they can no longer travel by that method but will crawl to adjacent forest regions in search of food.
During severe infestations, trees can become completely defoliated very rapidly. Most trees will die after one or two defoliations, thus eliminating a potential food supply for the growing moth population. Caterpillars seem to like certain trees better than others; oak trees are a preferred food but the caterpillars rarely ever eat tulip poplar trees.
Gypsy moth caterpillars are not affected by many standard predators since the larva usually hide during the day and eat only at night. There are some specific predators which may eventually create a natural balance, but human intervention is an important factor in minimizing primary forest damage in eastern forests. Some human methods of control include destroying egg masses, trapping caterpillars, and spraying trees with biological or chemical controls.
As with any good scientific research, it is important to survey available literature on the subject to review what has been done previously, and to establish precise parameters for an accurate simulation. A more thorough research of Gypsy Moths is recommended before building a realistic model, but the information provided above is probably sufficient to get a prototype started.
| A first stage of development in a Gypsy moth simulation would be to model a simple, closed population of moths with a standard birth rate and unlimited food supply. The time step could be done on a daily basis, but probably a yearly summary of Gypsy moth statistics would be sufficient since the desired outcome of this project is to show the qualitative behavior of a population over a long period of time. The expected behavior of this first stage would be to make certain that the model shows a typical exponential growth curve such as that shown in Figure #4. Gradually, other characteristics should be added, and the accuracy checked each time against expected behavior of the population. Figure #5 shows a repeated collapse of the Gypsy moth population due to overpopulation and starvation when all of the food supply is consumed. |
 Figure #4: Exponential Curve  Figure #5: Oscillating Growth |
There are always random factors which affect such simulations, but it is important to avoid adding random occurrences until all aspects of the model have been validated. Early introduction of random numbers to make things "interesting" should definitely be avoided. It is usually very difficult to determine whether the behavior of a model is the result of the randomness, or the result of complex interactions among other factors in the simulation. Constant values within an expected range should be used initially to prove the model is working correctly. Random numbers can always be added later.
It will be necessary to maintain much information about each of the cells, such as the number of caterpillars, birth rates, death rates, food supply, types of trees, history of past defoliations, the existence of predators, and spraying programs. Huge arrays of data will be required to keep track of all the important information available for a large number of cells.
This problem could now become too large for a typical supercomputer run if the same graphics visualization technique used in the trajectory model is applied here. To use every pixel on the screen as a separate cell would require extensive amounts of memory which might not be practical. A better approach in this case would be to divide the screen into small squares or other geometric shapes where each polygon stands for the status of a small segment of the overall population. With fewer cells and lower data requirements, it might be possible to accumulate information for successive years and display results as an animation over time.
Figures #6, #7, and #8 show various stages of the cellular
automaton approach to the simulation. The darker the color within
a cell, the greater the number of Gypsy moths in that region.
 Figure #6: Intitial Gypsy Moth Population 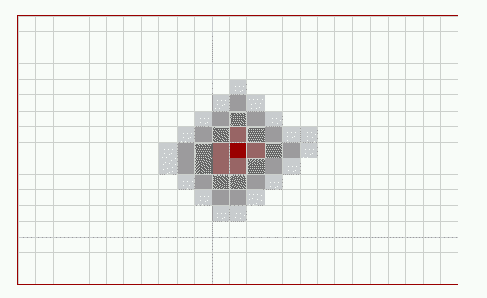 Figure #7: Expanding Population 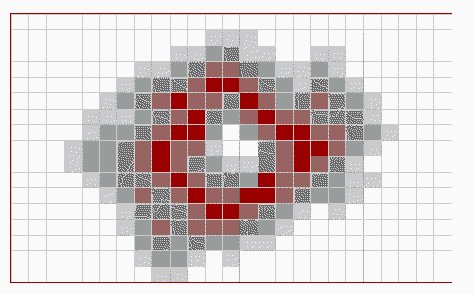 Figure #8: Collapsing Population |
Some possible projects for investigation include: