N-Body program, non-parallel version

  • Background material

    gravitytest1.c (C++ version gravitytest1.cpp) shell program of a sequential (non-parallel) version of the n-body algorithm using 3 particles. Here's a version using 2 particles, gravity2.c. These are C and C++ versions adapted for our class from these two UNC sites: N-body particle system and BSP N-body particle system

    An array of particle objects is used with:

    1. x,y position
    2. mass
    3. velocity components in the x and in the y directions
    Calculations are made of the gravitational force that all particles exert on each other at each time step. The gravitational force affects the x and y velocity components at each time step. The x and y velocity components change the x and y position of each particle at each time step. Time steps are simulated with a for loop, each iteration representing one time step.

  • First steps: Graphing results with Gnuplot (more help with gnuplot)
    1. Compile and run (do this on your workstation, Cray not needed here) gravitytest1.c - gcc gravitytest1.c -lm, (OR - use the C++ version, gravitytest1.cpp, g++ gravitytest1.cpp -lm) and run with a.out. This generates an ouput file of the motion of 3 particles, the x,y positions of each.

      The particles initial velocities particle.vx and particle.vy are 0 (these represent the velocities in the x and y directions. The mass of each particle is 100000000. The initial x,y location of the 3 particles (particle.px and particle.py) are (0,0), (0,5.0), (2.5, 4.33) - points in the shape roughly of an equalateral triangle. The program runs for 100 time steps.

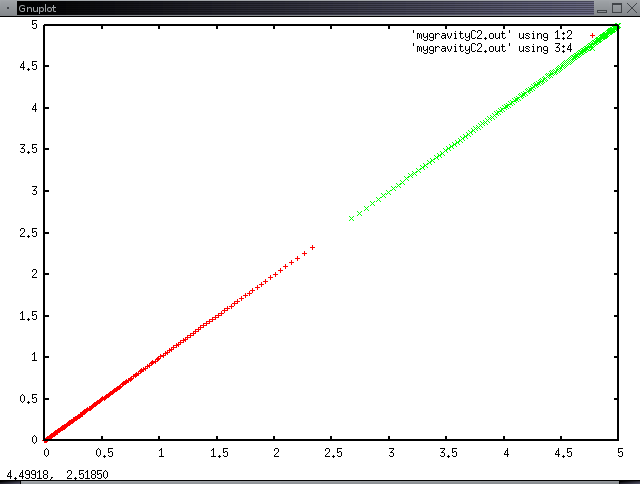
    2. To generate a text file of the x,y point locations of these 3 points over 100 time steps: ./a.out > gravity3.out. This statement writes the output to the text file gravity3.out. This file has 6 columns representing the x,y positions of the 3 points.

    3. Plot these point positions with Gnuplot:
      • gnuplot starts Gnuplot
      • plot 'gravity3.out' using 1:2, 'gravity3.out' using 3:4, \
        'gravity3.out' using 5:6;         (The backslash is used to continue a line in Gnuplot)
      • You'll see the tracks of the 3 particles toward a center point. Note the accelerations and decelarations (widening/shortening distances between points). The points come together, then pass each other for a short distance. This is only 100 steps.
      • Compile and run gravity2.c which runs for 180 time steps and uses 2 particles beginning at 0,0 and 5,5. The particles begin to accelerate toward each other.
      • Use exit to leave Gnuplot. Also - the up arrow repeats previous commands - save yourself typing!

    Plot for gravity3.c, 100 time steps, 3 particles initially at (0,0),(0,5), (2.5,4.33):

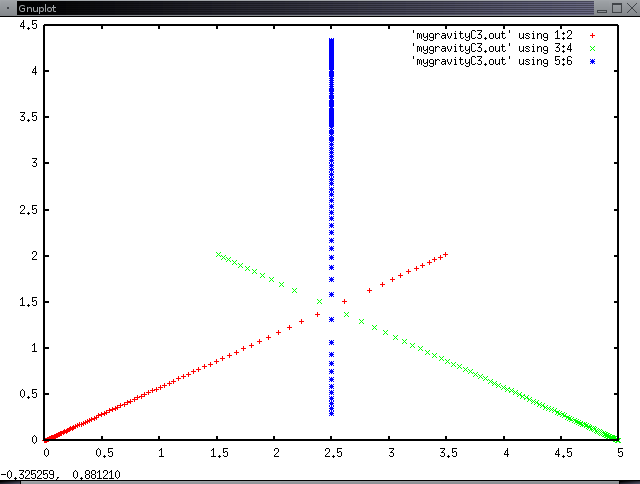
    Plot for gravity2.c, 180 time steps, 2 particles initially at (0,0) and (5,5):

  • Assignment

    1. Perform these 1st experiments above with 2 and 3 particles. Can you determine if the particles eventually come back together after passing each other?
    2. Perform experiments with more than 3 particles in order to graph the behavior of the system with Gnuplot.
    3. Can you make the points behave in curved fashion? Experiment with 2 points, one (the Sun) with large mass, the other (Earth) with smaller mass. Can you make the Earth approximate an orbit.

      For example, to help you start try gravitytestOrbitC.c: Mass 1 at (0,0) has mass 100000000, Mass 2 at (0,5) has mass 100 and an initial y velocity of 0.04. Run this for 1200 time steps. ./a.out > orbit1.out. In gnuplot use: 

         gnuplot> set xrange [-10:10];
   gnuplot> set yrange [-10:10];
   gnuplot> plot 'orbit1.out' using 1:2, 'orbit1.out' using 3:4;
      You should get an image such as:

    4. Try for more "planets" orbiting this "sun". Is the sun's position affected by the planets?

    5. OpenGL version of the tri-system: P1 at (0,0), P2 at (0,5), and P3 at (2.5, 4.33). All of these points have mass 100000000.

      gravitytestOpengl.c or gravitytestOpengl.cpp Use the following to compile this OpenGL program (C version): 

      ./lgcc gravitytest1Opengl.c
./a.out


Here's the file for lgcc:
#!/bin/sh
gcc $1 -lm -L/usr/lib -lGLU  -lGL -lglut  -L/usr/X11R6/lib -lX11 -lXext -lXi -lXmu

Use chmod 755 lgcc
inorder to make this executable

      For the CPP version use: 

      ./lg++ gravitytest1Opengl.cpp
./a.out


Here's the file for lg++:
#!/bin/sh
g++ $1 -lm -L/usr/lib -lGLU  -lGL -lglut  -L/usr/X11R6/lib -lX11 -lXext -lXi -lXmu

Use chmod 755 lg++
inorder to make this executable

    6. Now try your orbital version in OpenGL

    7. Two sets of 3 points, each set forms an equilateral triangle: gravity7.c". These six points are

      (1,3), (4,3), (2.5, 3.6) - first triangle pattern

      (6,3), (9,3), (7.5, 3.6) - second triangle pattern

      Use the following Gnuplot commands: 

      
gnuplot> set xrange[-1:10];
gnuplot> set yrange[-1:10];

gnuplot> plot 'gravity7.out' using 1:2, 'gravity7.out' using 3:4, \
> 'gravity7.out' using 5:6, 'gravity7.out' using 7:8, \     
> 'gravity7.out' using 9:10, 'gravity7.out' using 11:12;

      The image should look like:

    8. OpenGL version of 6 points (2 triangles), gravitytest2Opengl.c (lgcc gravitytest2Opengl.c, then ./a.out)

    9. Can you find a combination of masses and/or initial velocities that result in a relatively stable system.