AI Spring 2009
Neural Network Programming

1. Machine Learning AI web site

2. Lab Warmup, Constructing a Perceptron (optional beginning step)
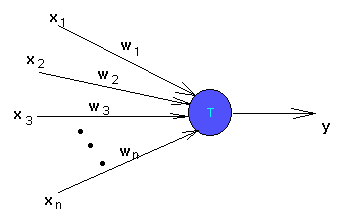
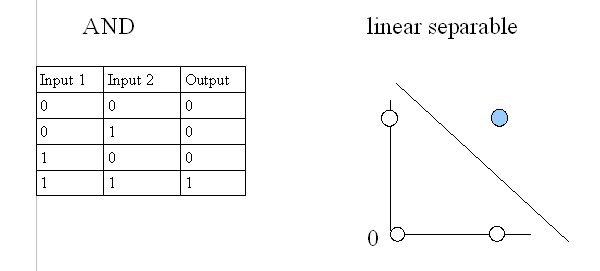
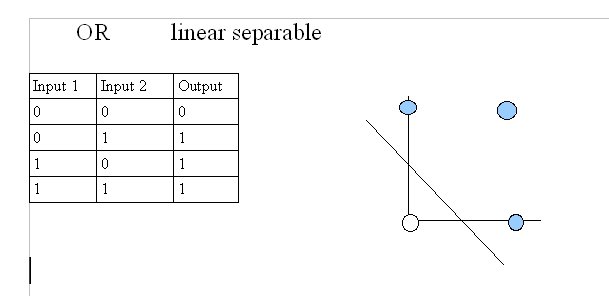
   • The simplest neural net structure, the perceptron, only can train and learn using linear separable functions such as AND, OR

   • Lab1 Intro1 An initial description of the perceptron xor problem from www.iiit.net/~vikram/nn_intro.html

     A perceptron (from the above website)

     

     Linear separable AND, OR:

     

     

   
   

3. Lab 1 - Develop a trainable neural net structure to learn the XOR function. (non linear separable)

   

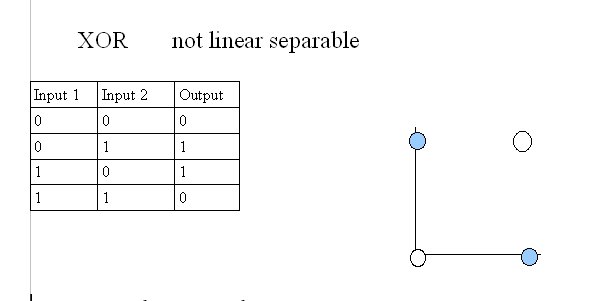
   Your neural net should take 2 inputs, 0 or 1, and learn to output the correct value according to the XOR function:

   

   

   

   

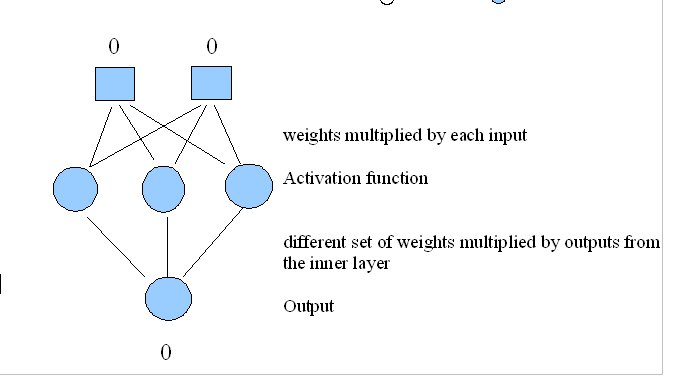
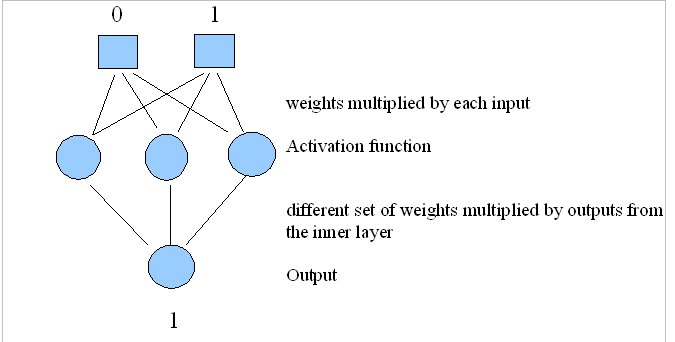
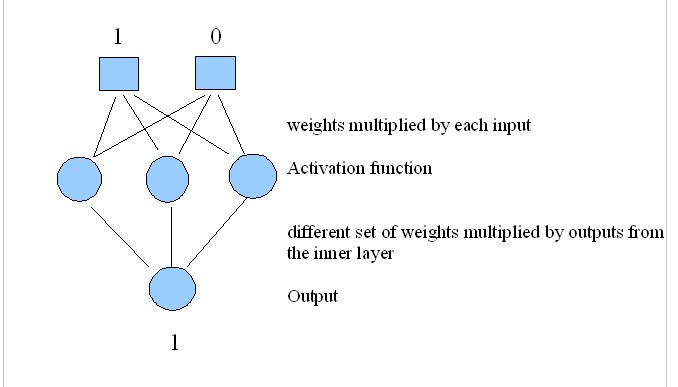
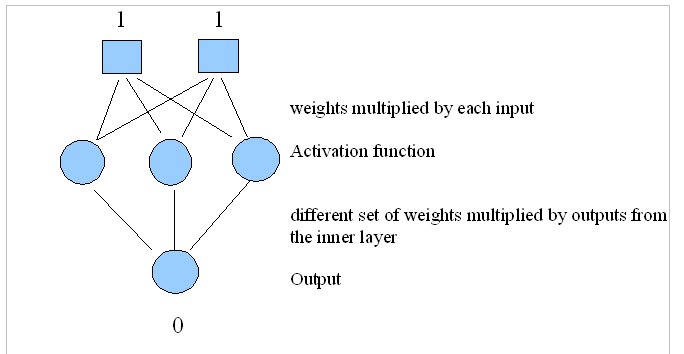
   Find suggested weights on our Machine Learning website, and weights.txt

4. Lab 1 and Lab 2 neural network structures:
   • Lab1 Structure and sample output
   • Lab2 Structure
   • AI website for weights files for weights1.txt and weights_generalized_2.txt

   Lab 1

   

   
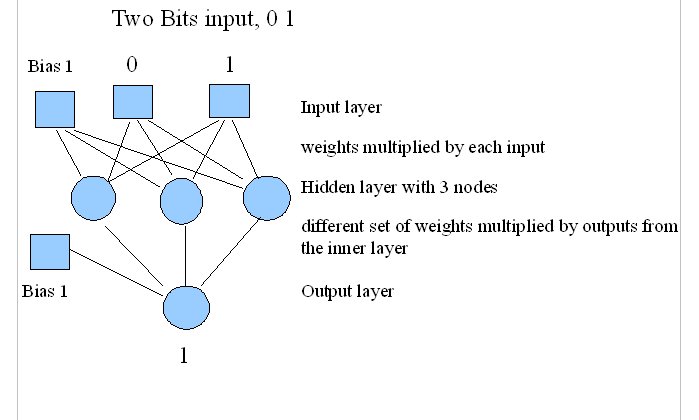
   Lab 2 structure:

   

5. Lab 2B (lab 2 revisited) Neural net, Feedforward XOR (two inputs and one output) using given weights, two hidden layers with four and three nodes, plus bias on input and hidden layers.
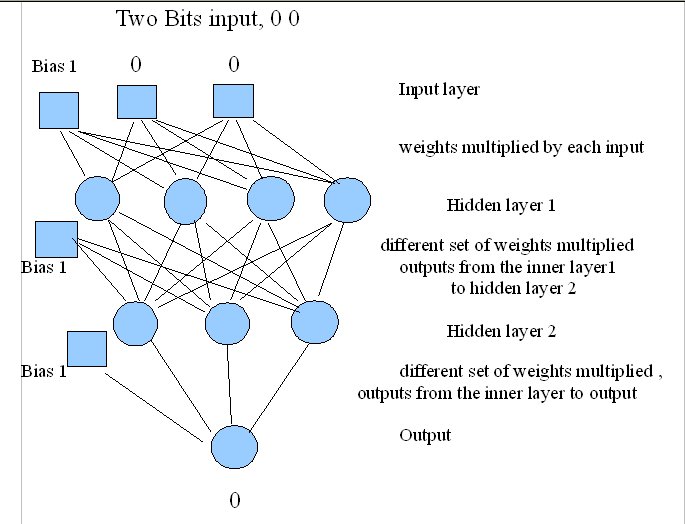
   • see the machine learning ai website
   • Verify your feedfoward neural net works with XOR and the following sets of weights
     • weights_generalized_2.txt
     • weights_generalized_3.txt
     • weights_jiggled_1.txt
     • weights_jiggled_2.txt
     • weights_jiggled_3.txt

6. LAB 3 INTRO Assignment...THIS JUST IN!: Senior Challenge (on your last day) and Underclass another assignment -
   DO THIS BEFORE LAB 3 (if you haven't already done Lab 3)
   • See Handout - Practice on adjusting weights for a perceptron - no hidden layer

   • 	   # Torbert shell program for a simplified learning process
     
     	   # Negation: x1=1 then z=0, x1=0 then z=1
     
     	   # No hidden layer (perceptron) so feed-forward (ff) is just a evaluation function
     
     	   # Network structure:
     	   #  BIAS      INPUT
     	   #   \          /
     	   #    w0       w1
     	   #     \      /
     	   #      OUTPUT
     	   
     	   x0=1    # bias, constant term in linear equation  
     
     	   w0=random()    # weight connecting bias to output
     	   w1=random()    # weight connecting input to output
     
     	   def ff(x1):  # Feed-forward has no loops since the network is so simple
     	     # Weighted sum is from input layer directly to output layer
     	     # Activation function is the logistic sigmoid
     	     ....see more code on handout
     	     
     	     z=1.0/(1.0+exp(y))
     
     	   return z
     					   
     	   print "Initial weights: w0=%0.3f and w1=%0.3f" % (w0,w1)
     	   print				   
     	   print "Learning..."
     	    #
     	    #
     	    #  Your code goes here
     	    #
     	    #
     	    print "Done!"
     	    print
     	    print "Learned weights: w0=%0.3f and w1=%0.3f" % (w0,w1)
     	    print
     	    while True:
     		input = raw_input("Enter 0 or 1: ")
     		if input =='q':
     		   break
     		if input not in ['0','1']:
     		   continue
     		input = int(input)
     	        output=ff(input)
     		print "Negation of %d is %d (%0.3f)" % (input, int(0.5+output),output)
     		print
     	   print "bye"
     	   

7. Lab 3: Designing your own network, begin with arbitrary weights, adjust the arbitrary weights n times in order to get a desired output.
   • Input: 1 0 1 bias
   • Output: 0 1
   • you choose the number of hidden layers
   • you choose the number of nodes in each hidden layer
   • Lab 2 revisited and Lab 3 overview
   • Lab3 Structure
   • Use the feedforward process outlined by Mr. Torbert

        Loop-epoch  keep looping this process until you are close enough to the desired output
     
                      output    input  for feedforward results with weights    
                        
            error = | correct - ff(w1,w2,w3,...) |  or use 1/2(        )^2
                                                       rather than absolute value
     
            loop for each weight
                                            0.1 for example
     	      
              error' = | correct - ff(w1 + delta w, w2, w3,...) | or use 1/2(     )^2
                                                                    rather than
     		                                              absolute value
     		 d Error         error' - error
     		 -------     =   -------------
     		 d weight          delta w 
     
            
     
            loop for each weight
     
     	   Weight new = Weight old - 0.8( d Error/d weight)
     
     	   			    Use some factor such as 0.8,
     				     or 0.5, or 0.1, ...
        

8. Lab 4 Use a backpropagation process to calculate the adjustment of the weights in order to achieve the desired output. Use a 0 hidden layer network.

   

   

9. Lab 5 (this may be extra) Use a backpropagation process to calculate the adjustment of the weights in order to achieve the desired output. Use a 1 hidden layer network.
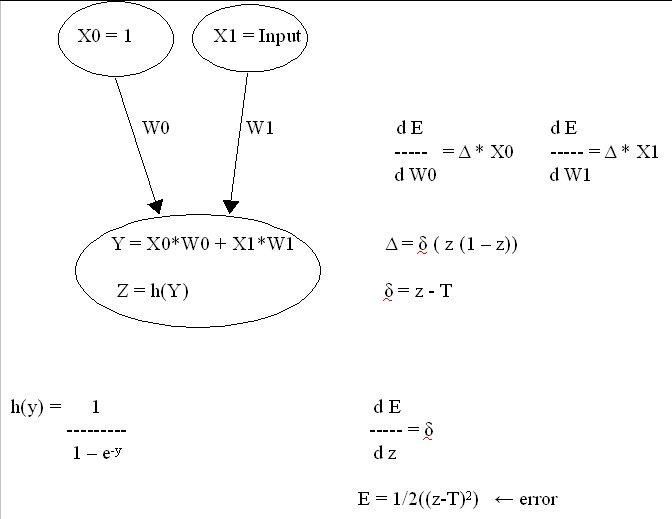
   • --Use the Mr. Torbert's explanatory diagram and handout for a neural structure with 1 input, 1 hidden layer with two nodes, 1 output node

                          X0 (bias)     X1 (input)
     
     	    X (bias) 	hidden      hidden
     			node 0      node 1
     
                             
                                  output
     			     node
     		

10. youtube neural networks overview from Indian Institute of Technology and Science